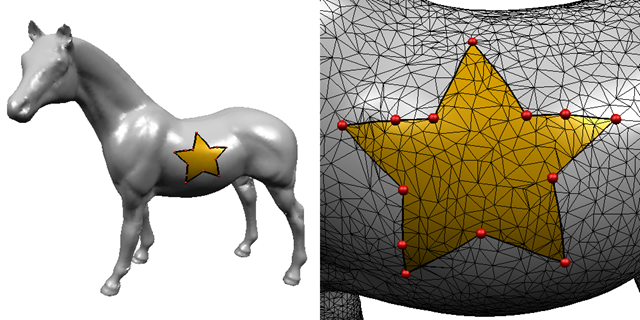
A new algorithm is proposed for calculating the approximate shortest path on a polyhedral surface. The method mainly uses Dijkstra’s algorithm and is based on selective refinement of the discrete graph of a polyhedron. Although the algorithm is an approximation, it has the significant advantages of being fast, easy to implement, high approximation accuracy, and numerically robust. The approximation accuracy and computation time are compared between this approximation algorithm and the extended Chen & Han (ECH) algorithm that can calculate the exact shortest path for non-convex polyhedra. The approximation algorithm can calculate shortest paths within 0.4% accuracy to roughly 100-1000 times faster than the ECH algorithm in our examples. Two applications are discussed of the approximation algorithm to geometric modeling.
Papers
- Takashi Kanai, Hiromasa Suzuki: “Approximate Shortest Path on a Polyhedral Surface and Its Applications”, Computer Aided Design, Volume 33, Number 11, pp.801-811, September 2001.
- Takashi Kanai, Hiromasa Suzuki: “Approximate Shortest Path on a Polyhedral Surface Based on Selective Refinement of the Discrete Graph and Its Applications”, Proc. Geometric Modeling and Processing 2000, pp.241-250, IEEE CS Press, Los Alamitos, CA, April 2000. [pdf (664KB)]
Code