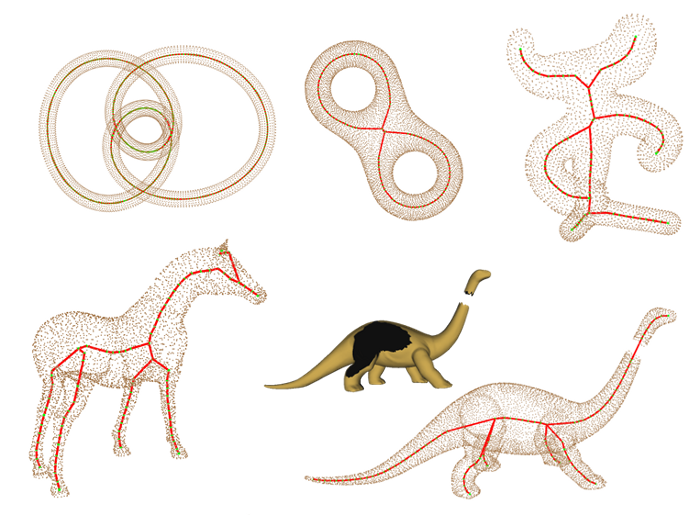
A curve skeleton of a 3D object is one of the most important structures of the object, which is extremely useful for many computer graphics applications involving in shape analysis. Much research has focused on volumetric and polygonal mesh models. However, only a few have been paid attention to point cloud and suffered from several limitations such as connectivity or inside-shape information requirements, difficulty to compute junction nodes, or inappropriate parameter tuning. To resolve these problems, we propose an effective algorithm for extracting a robust and centered curve skeleton from point cloud. The process starts from estimating centers of antipodes of a point cloud, so called skeletal candidates, which are fundamentally inside the shape; but scattered. We thus filter and shrink them to create less-noisy skeletal candidates before applying one-dimensional Moving Least Squares (MLS) to build a thin point cloud. The latter is then downsampled to sparse skeletal nodes. With recent nodes, it is possible to create a smooth curve skeleton; but distorted due to shrinking and thinning (MLS) processes. We thus utilize cross-section plane technique and least squares ellipse fitting to relocate skeletal nodes to create a centered curve skeleton. The algorithm is validated on many complex models ranging from cylindrical to planar ones, and from clean to noisy and incomplete data. We show that the extracted curve skeleton is robust to noises and under centeredness property.
Papers
- Vanna Sam, Hiroaki Kawata, Takashi Kanai: “A Robust and Centered Curve Skeleton Extraction from 3D Point Cloud”, Computer-Aided Design and Applications, Vol.9, No.6, pp.869-879, 2012.