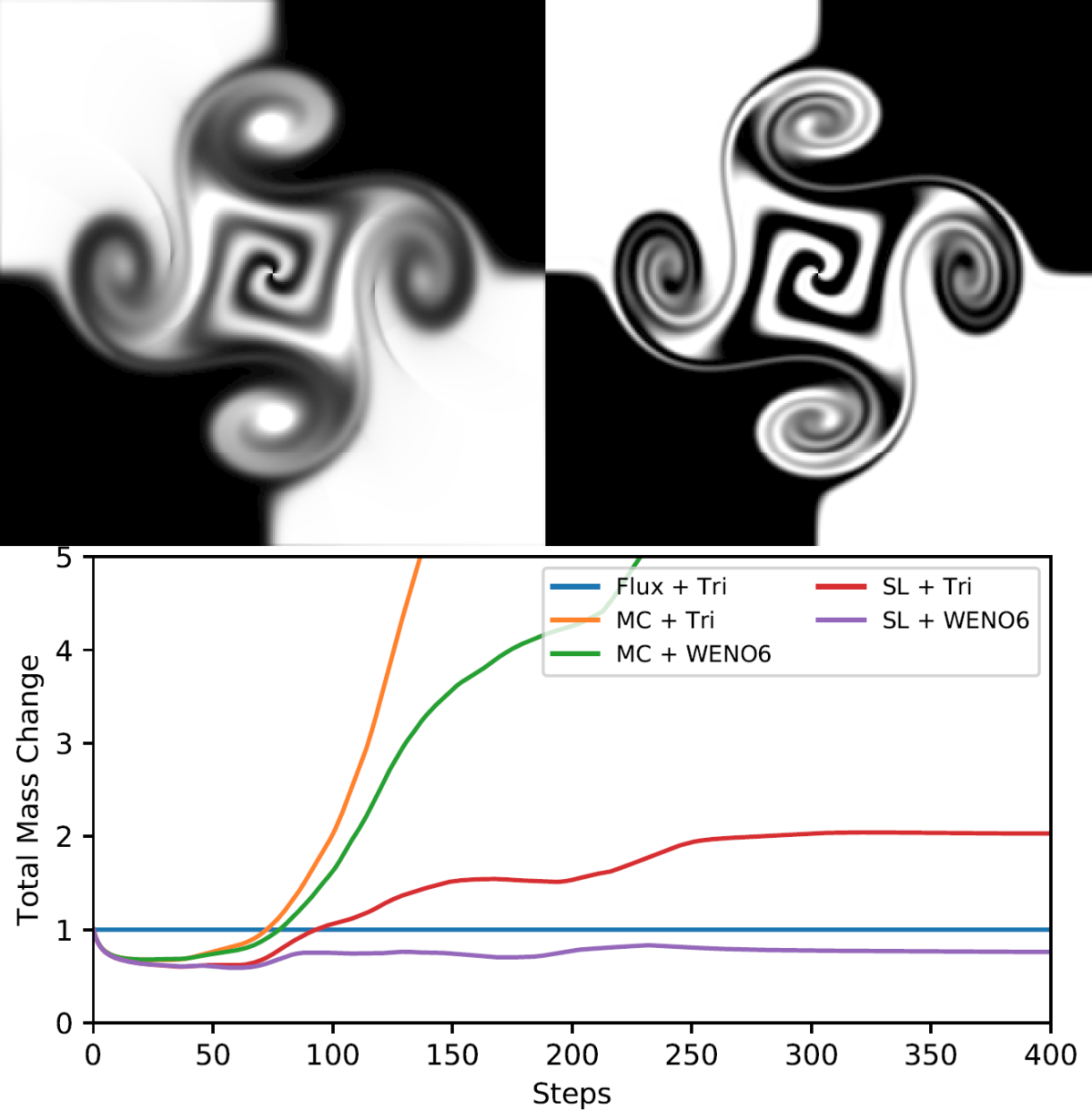
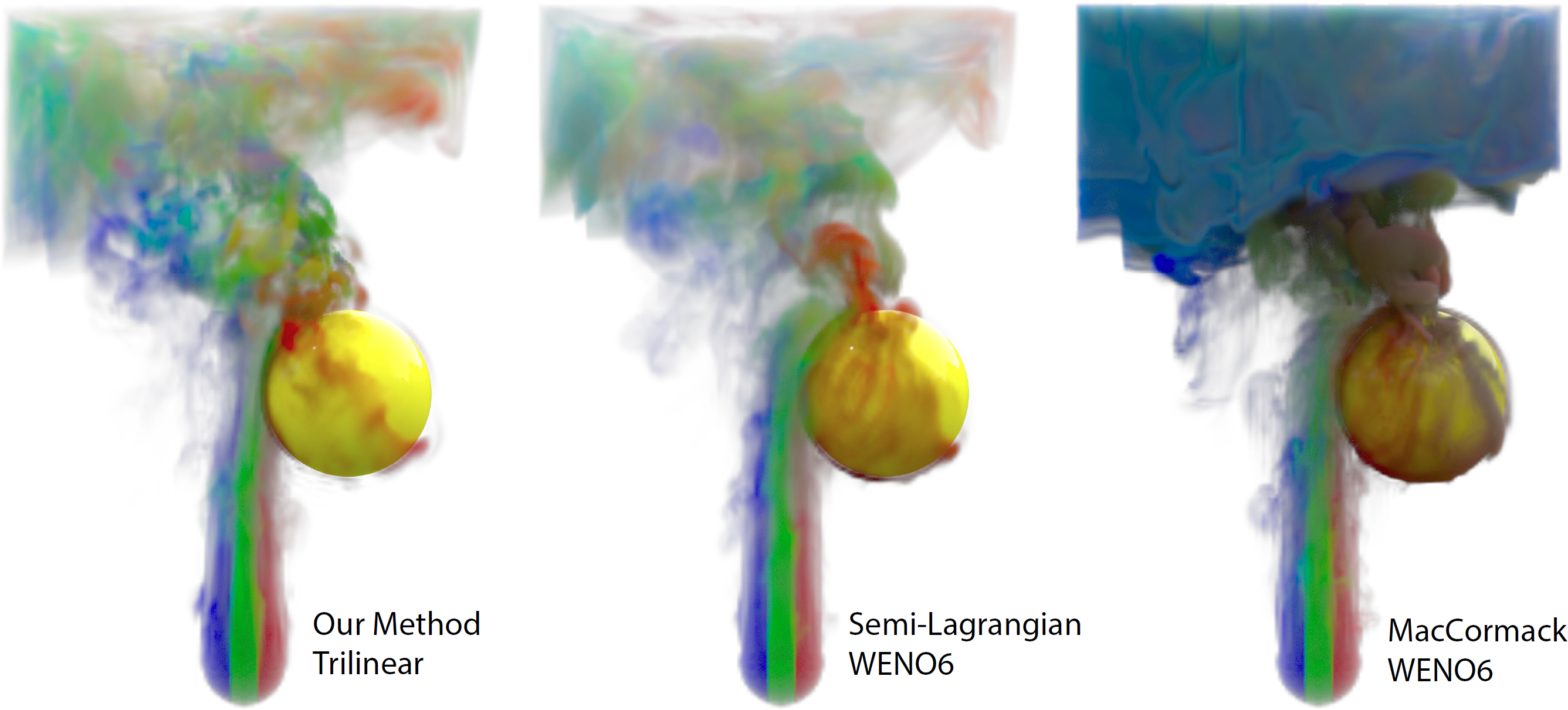
We propose a new advection scheme for fluid simulation that improves both conservation and numerical diffusion. Our work differs from previous works in that we re-formulate interpolation as the cell-face flux of a vector field instantly constructed from a scalar field, rather than a per-point evaluation at back-traced positions. Our novel interpolation method enables excellent preservation of conservative quantities since the sum of flux exactly counteracts on cell faces, which eventually evaluates the boundary-flux of the whole domain. Our method can be implemented as a plug-and-play extension (or a temporary scratchpad) to the conventional semi-Lagrangian scheme; hence, our method naturally inherits all the benefits of semi-Lagrangian schemes and can be seamlessly integrated with existing fluid simulation pipelines together with other (black-boxed) solver components.
The project page is here.
Papers
- Naoyuki Hirasawa, Takashi Kanai, Ryoichi Ando: “A Flux-Interpolated Advection Scheme for Fluid Simulation”, The Visual Computer (Special issue for CGI 2021), Volume 37, Issues 9-11, pp.2607-2618, 2021.