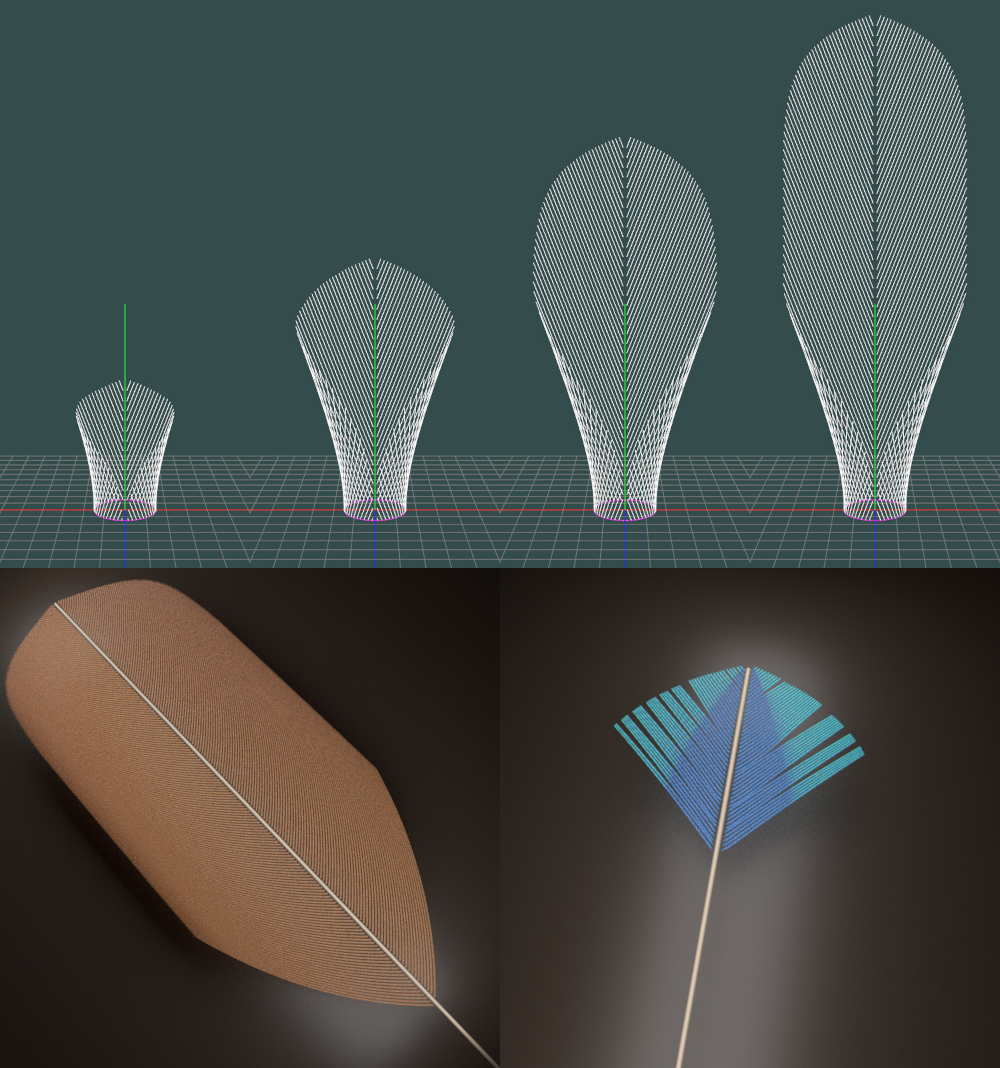
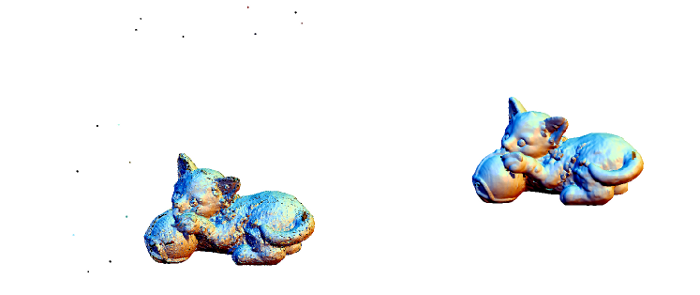羽毛は,シャフトから分岐する巨大な繊維の曲線(羽枝と呼ばれる)を伴う,鳥の皮膚上の洗練された皮膚の付属器官である.羽枝は,その小鉤(小羽枝と呼ばれる)を利用し,さらに互いに噛み合い,2つの表面を形成している.本研究では,自然の羽の発達に倣った生物学的モデル化手法を提案し,共通の生物学的特徴を手続き的 … “形態発生シミュレーションを用いた CGのための羽の生物学的モデリング” の続きを読む
カテゴリー: 幾何形状モデリング
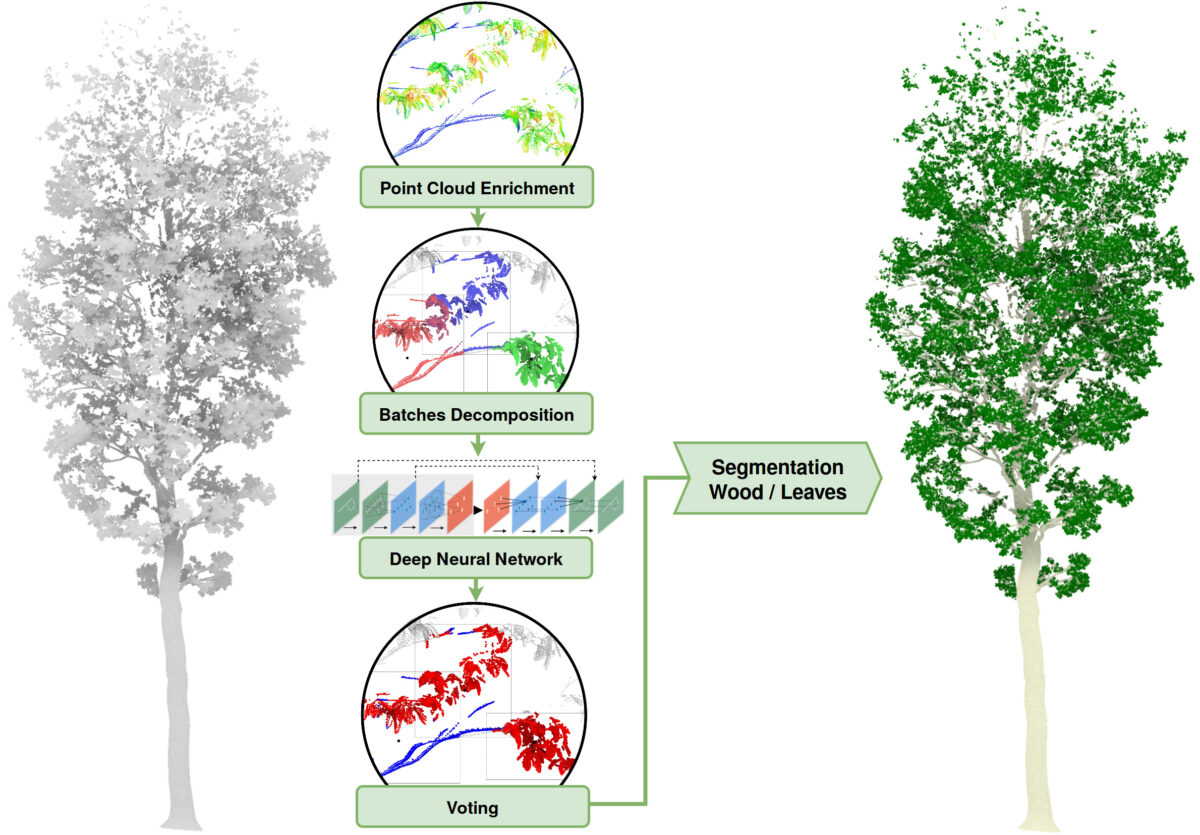
不均衡かつ不均質な点群のセグメンテーションと測定木への適用
不均衡で不均質な 3 次元点群に対するセグメンテーションは未解決の問題である.植物の木のモデリングの応用において,その基本的な課題は,木から葉を分離することである.本研究では,ディープラーニングとクラス決定プロセスに基づき,地上からの LiDAR 点群の木の葉と木の点を分離するために設計された新しい … “不均衡かつ不均質な点群のセグメンテーションと測定木への適用” の続きを読む
DenseGATs: キャラクタの非線形変形のためのグラフアテンションネットワーク
アニメーション制作において,アニメータは常に複雑な外見やディテールを持つキャラクターのための高品質な変形システムを開発するため,多大な時間と労力を費やしている.本研究では,スキニングと微調整の繰り返しに費やす時間を削減するため,高品質なスキニングを施したキャラクタのメッシュの既存のグラフ情報をもとに … “DenseGATs: キャラクタの非線形変形のためのグラフアテンションネットワーク” の続きを読む
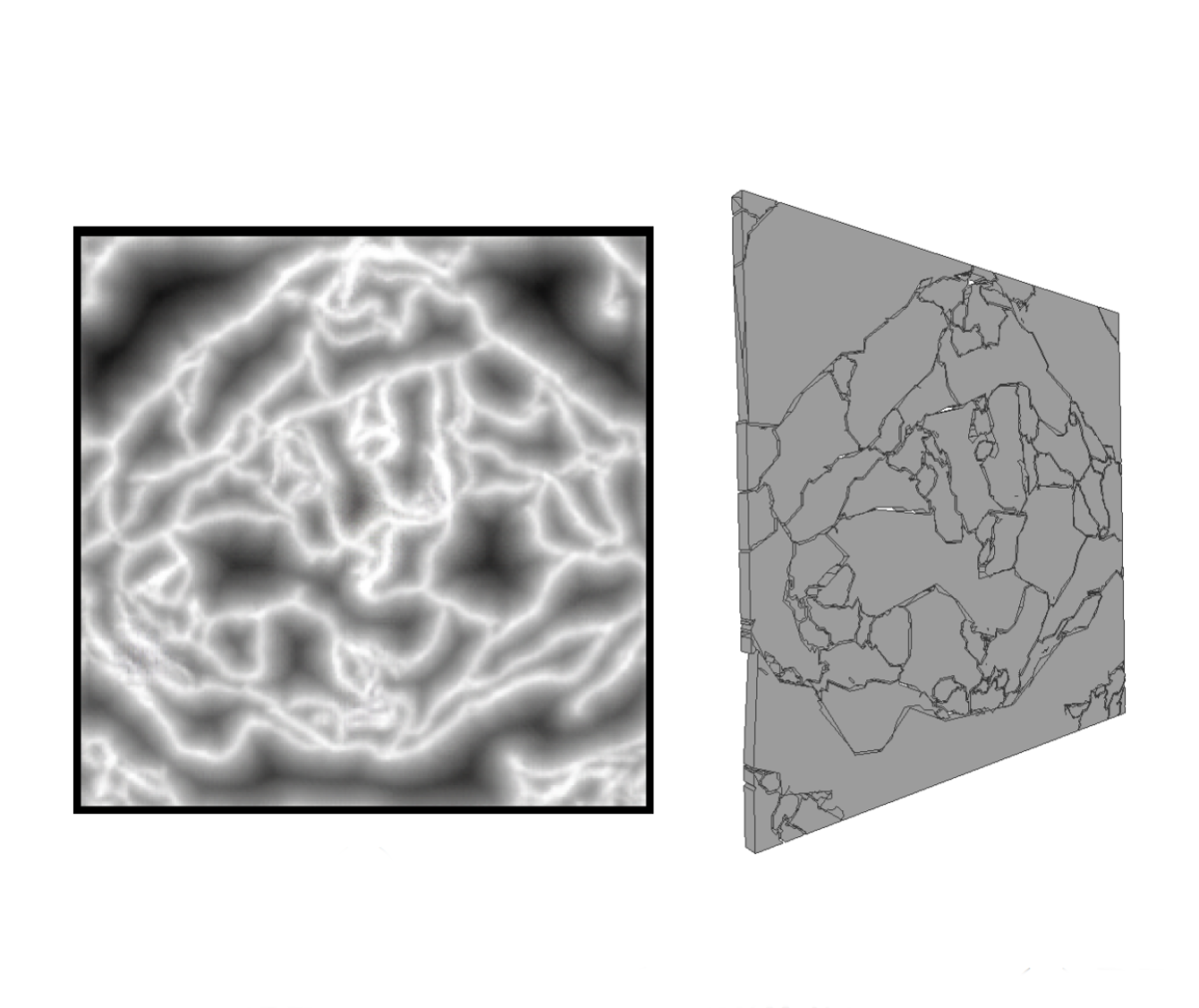
深層学習を用いた2D平面の脆性破壊形状生成
ガラスやコンクリートなどの平面形状の物体の脆性破壊は,現実世界でもよく見られる.剛体の破壊アニメーションは,物理指向のシミュレーションを用いることで,印象的な効果を得ることができる.しかし,現実的な破壊アニメーションを生成するために物理指向のシミュレーション手法を選択する場合,シミュレーションコスト … “深層学習を用いた2D平面の脆性破壊形状生成” の続きを読む
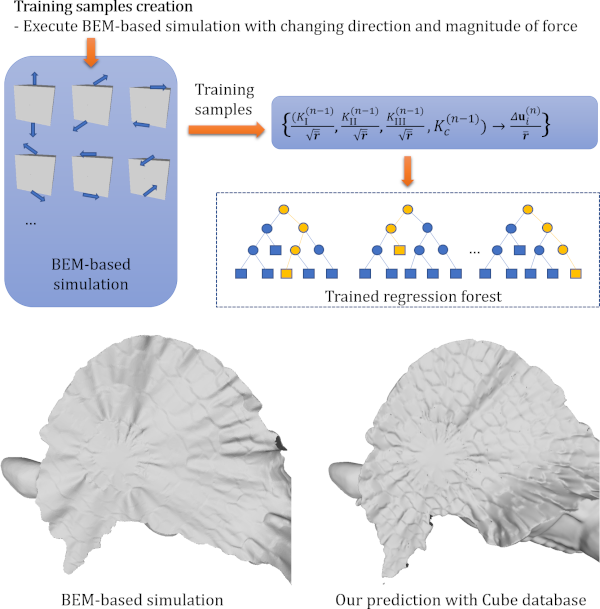
データ駆動法による脆性破壊曲面形状シミュレーション
脆性破壊曲面形状シミュレーションは,ゲームや映画の重要な課題として扱われている.脆性破壊に関する既存手法の中では,計算速度重視の手法と,リアリティ重視の手法がある.しかし,計算コストが高い物理ベースの手法の実現は長年解決できない問題であった.その中で,境界要素法 (BEM) を導入し,既存手法と比べ … “データ駆動法による脆性破壊曲面形状シミュレーション” の続きを読む
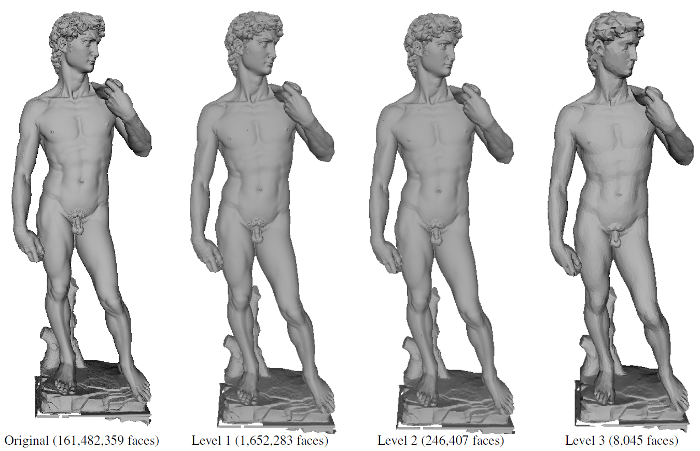
QEMメッシュ簡略化のためのアウトオブコアフレームワーク
エッジ縮退処理を繰り返し行うことで簡略化を行うインコア簡略化手法は,特徴的形状を保ち,かつ,高品質な簡略化メッシュを得られる手法であることが知られている.しかしながら,処理に必要とするメモリ消費量が非常に多く,一億ポリゴンを超えるような巨大なメッシュに対して適用するのは難しい.一方で,巨大メッシュを … “QEMメッシュ簡略化のためのアウトオブコアフレームワーク” の続きを読む
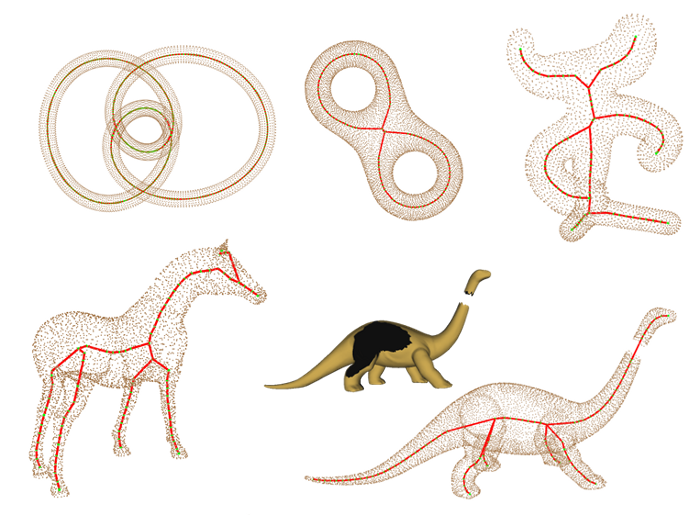
3次元点群からの頑健かつ中心を通る曲線スケルトンの抽出
3次元形状の曲線スケルトンは形状の最も重要な構造の一つであり,形状解析を含む多くのCG応用に対して極めて有用である.しかし,曲線スケルトンに関する多くの研究は,ボリュームデータやポリゴンメッシュを対象とするものである.点群からの抽出はそれほど考慮されていないだけでなく,接続情報や形状内部情報の欠如, … “3次元点群からの頑健かつ中心を通る曲線スケルトンの抽出” の続きを読む
点群に対する頑健な MLS 投影オペレータ
本研究では,外れ値を伴うようなノイズの多い点群に対する頑健な投影オペレータを提案する.このオペレータは,Moving Least Square (MLS) 投影の拡張であり,その平滑化における性質を継承している.キーとなるアイデアは,外れ値の影響を妨げるように平均値と投影方向を計算することにある.こ … “点群に対する頑健な MLS 投影オペレータ” の続きを読む
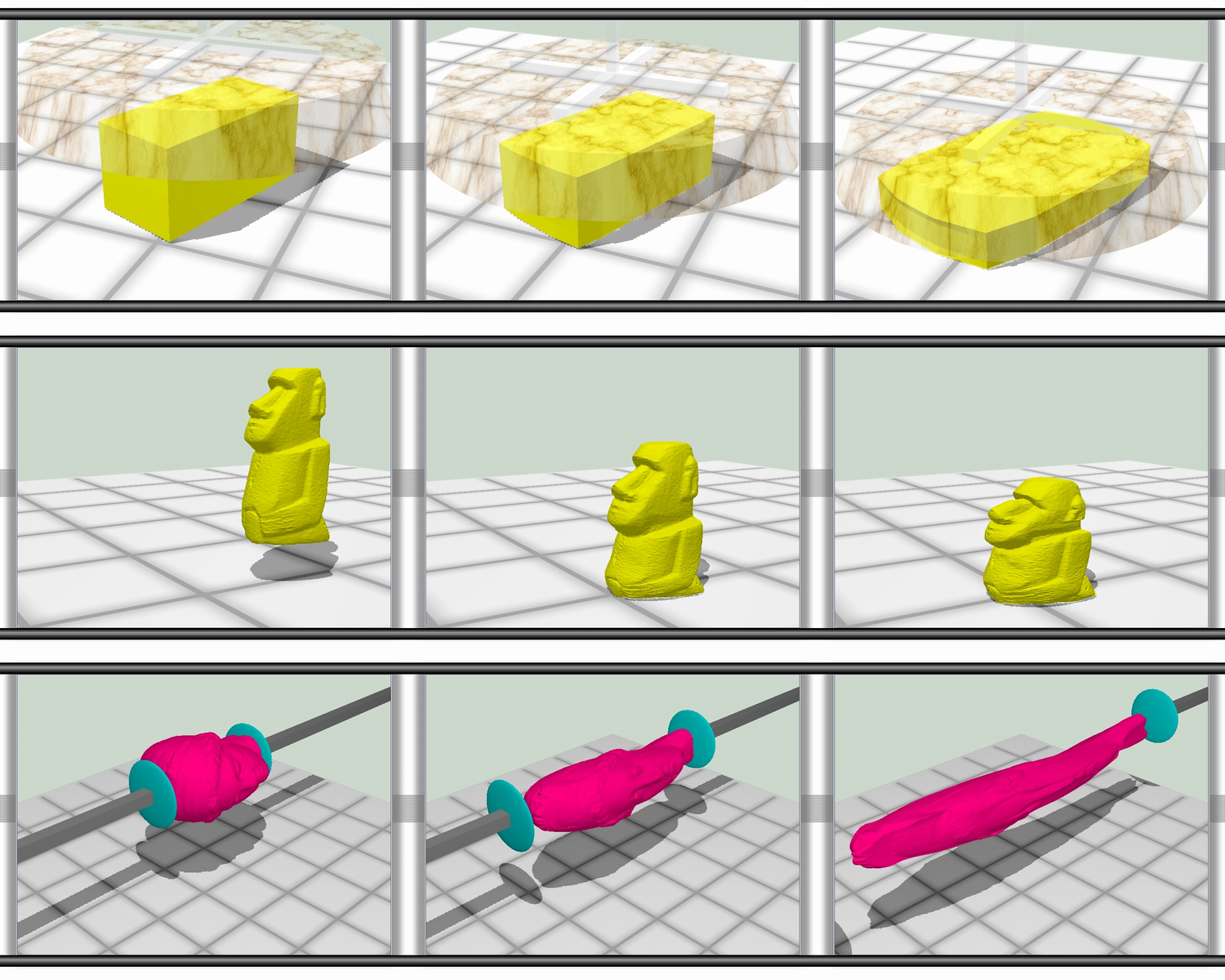
シェイプマッチング法による体積保存を考慮した形状変形手法
物理法則シミュレーションにもとづく形状変形は,3DCGアプリケーションにおいて人間の肌や布のような弾性変形を表現するために利用される.中でも,シェイプマッチング法は,弾性体のような動きを実現する高速かつ頑健な手法として注目されている.しかし,オリジナルのシェイプマッチング法では,体積が保存されないた … “シェイプマッチング法による体積保存を考慮した形状変形手法” の続きを読む
メッシュから陰関数曲面への誤差に基づく階層的近似
本論文は,ポリゴンメッシュから迅速かつ効率良く,陰関数曲面を生成する手法を述べている.ポリゴンから陰関数曲面への距離関数を新たに提案している.この関数は,ポリゴンへのタイトなフィッティングを実現できるほか,二次形式としてまとめることができるため,エネルギの保存・評価などに効率的である.また,本論文で … “メッシュから陰関数曲面への誤差に基づく階層的近似” の続きを読む