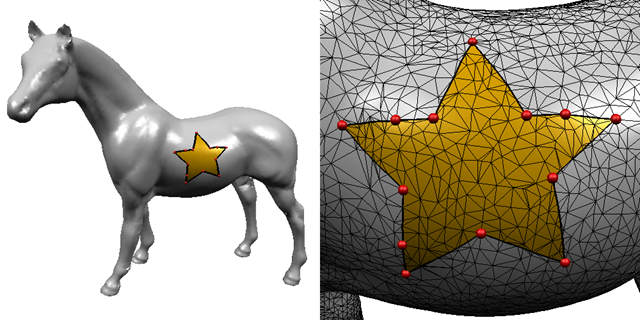
メッシュ上の近似最短経路を計算するための，新しいアルゴリズムについて提案する．本手法は主にダイクストラの手法を用い，多面体の離散グラフの選択的詳細化に基づく．このアルゴリズムは近似手法であるが，高速である，実装が簡単である，近似精度が高い，数値的に頑健である，などいくつかの重要な利点を持つ．また，本近似アルゴリズムと，非凸多面体の正確な最短経路を計算することのできる拡張 Chen & Han (ECH) アルゴリズムに対し，計算精度と計算時間に関する比較を行った．その結果，我々の例題では，ECH アルゴリズムに比べて 0.4% 以内の近似精度に収まる経路が，おおよそ 100-1000 倍の速さで求めることができた．さらに，本近似アルゴリズムの形状モデリングに対する二つの応用についても議論する．
論文
- Takashi Kanai, Hiromasa Suzuki: “Approximate Shortest Path on a Polyhedral Surface and Its Applications”, Computer Aided Design, Volume 33, Number 11, pp.801-811, September 2001.
- Takashi Kanai, Hiromasa Suzuki: “Approximate Shortest Path on a Polyhedral Surface Based on Selective Refinement of the Discrete Graph and Its Applications”, Proc. Geometric Modeling and Processing 2000, pp.241-250, IEEE CS Press, Los Alamitos, CA, April 2000. [pdf (664KB)]
- 金井 崇, 鈴木 宏正: “離散グラフの選択的詳細化に基づく多面体上の近似最短経路算出とその応用”, 情報処理学会 第 97 回 グラフィックスと CAD 研究会 (情報処理学会研究報告, Vol.99, No.105, 99-CG-97, pp. 13-18), 東京, 12 月, 1999.
ソフトウェア